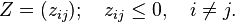Uncategorized – Page 10

2011/01/30

Z-matrix

the class of Z-matrices are those matrices whose off-diagonal entries are less than or equal to zero; that is, a Z-matrix Z satisfies

$Z=(z_{ij});quad z_{ij}leq 0, quad ineq j.$

Note that this definition coincides precisely with that of a negated Metzler matrix or quasipositive matrix, thus the term quasinegative matrix appears from time to time in the literature, though this is rare and usually only in contexts where references to quasipositive matrices are made.

The Jacobian of a competitive dynamical system is a Z-matrix by definition. Likewise, if the Jacobian of a cooperative dynamical system is J, then (−J) is a Z-matrix.

Related classes are L-matrices, M-matrices, P-matrices, Hurwitz matrices and Metzler matrices. L-matrices have the additional property that all diagonal entries are greater than zero. M-matrices have several equivalent definitions, one of which is as follows: a Z-matrix is an M-matrix if it is nonsingular and its inverse is nonnegative. All matrices that are both Z-matrices and P-matrices are nonsingularM-matrices.

2011/01/30

M-matrix

An M-matrix is a Z-matrix with eigenvalues whose real parts are positive. M-matrices are a subset of the class of P-matrices, and also of the class of inverse-positive matrices (i.e. matrices with inverses belonging to the class of positive matrices).^[1]

A common characterization of an M-matrix is a non-singular square matrix with non-positive off-diagonal entries and all principal minors positive, but many equivalences are known. The name M-matrix was seemingly originally chosen by Alexander Ostrowski in reference to Hermann Minkowski.^[2]

A symmetric M-matrix is sometimes called a Stieltjes matrix.

M-matrices arise naturally in some discretizations of differential operators, particularly those with a minimum/maximum principle, such as the Laplacian, and as such are well-studied in scientific computing.

The LU factors of an M-matrix are guaranteed to exist and can be stably computed without need for numerical pivoting, also have positive diagonal entries and non-positive off-diagonal entries. Furthermore, this holds even for incomplete LU factorization, where entries in the factors are discarded during factorization, providing useful preconditioners for iterative solution.

2011/01/28

Gram–Schmidt process

the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly theEuclidean space Rⁿ. The Gram–Schmidt process takes a finite, linearly independent set S = {v₁, …, v_k} for k ≤ n and generates an orthogonal set S′ = {u₁, …, u_k} that spans the same k-dimensional subspace of Rⁿ as S.

The method is named for Jørgen Pedersen Gram and Erhard Schmidt but it appeared earlier in the work of Laplace and Cauchy. In the theory of Lie group decompositions it is generalized by theIwasawa decomposition.

The application of the Gram–Schmidt process to the column vectors of a full column rank matrix yields the QR decomposition (it is decomposed into an orthogonal and a triangular matrix).

The Gram–Schmidt process

We define the projection operator by

$mathrm{proj}_{mathbf{u}},(mathbf{v}) = {langle mathbf{v}, mathbf{u}rangleoverlangle mathbf{u}, mathbf{u}rangle}mathbf{u} ,$

where 〈u, v〉 denotes the inner product of the vectors u and v. This operator projects the vector v orthogonally onto the vector u.

The Gram–Schmidt process then works as follows:

$begin{align} mathbf{u}_1 & = mathbf{v}_1, & mathbf{e}_1 & = {mathbf{u}_1 over |mathbf{u}_1|} \ mathbf{u}_2 & = mathbf{v}_2-mathrm{proj}_{mathbf{u}_1},(mathbf{v}_2), & mathbf{e}_2 & = {mathbf{u}_2 over |mathbf{u}_2|} \ mathbf{u}_3 & = mathbf{v}_3-mathrm{proj}_{mathbf{u}_1},(mathbf{v}_3)-mathrm{proj}_{mathbf{u}_2},(mathbf{v}_3), & mathbf{e}_3 & = {mathbf{u}_3 over |mathbf{u}_3|} \ mathbf{u}_4 & = mathbf{v}_4-mathrm{proj}_{mathbf{u}_1},(mathbf{v}_4)-mathrm{proj}_{mathbf{u}_2},(mathbf{v}_4)-mathrm{proj}_{mathbf{u}_3},(mathbf{v}_4), & mathbf{e}_4 & = {mathbf{u}_4 over |mathbf{u}_4|} \ & {} vdots & & {} vdots \ mathbf{u}_k & = mathbf{v}_k-sum_{j=1}^{k-1}mathrm{proj}_{mathbf{u}_j},(mathbf{v}_k), & mathbf{e}_k & = {mathbf{u}_kover |mathbf{u}_k |}. end{align}$

The first two steps of the Gram–Schmidt process

The sequence u₁, …, u_k is the required system of orthogonal vectors, and the normalized vectors e₁, …, e_k form an orthonormal set. The calculation of the sequence u₁, …, u_k is known as Gram–Schmidt orthogonalization, while the calculation of the sequence e₁, …,e_k is known as Gram–Schmidt orthonormalization as the vectors are normalized.

To check that these formulas yield an orthogonal sequence, first compute 〈u₁, u₂〉 by substituting the above formula for u₂: we get zero. Then use this to compute 〈u₁, u₃〉 again by substituting the formula for u₃: we get zero. The general proof proceeds bymathematical induction.

Geometrically, this method proceeds as follows: to compute u_i, it projects v_i orthogonally onto the subspace U generated by u₁, …,u_i−1, which is the same as the subspace generated by v₁, …, v_i−1. The vector u_i is then defined to be the difference between v_i and this projection, guaranteed to be orthogonal to all of the vectors in the subspace U.

The Gram–Schmidt process also applies to a linearly independent infinite sequence {v_i}_i. The result is an orthogonal (or orthonormal) sequence {u_i}_i such that for natural number n: the algebraic span of v₁, …, v_n is the same as that of u₁, …, u_n.

If the Gram–Schmidt process is applied to a linearly dependent sequence, it outputs the 0 vector on the ith step, assuming that v_i is a linear combination of v₁, …, v_i−1. If an orthonormal basis is to be produced, then the algorithm should test for zero vectors in the output and discard them because no multiple of a zero vector can have a length of 1. The number of vectors output by the algorithm will then be the dimension of the space spanned by the original inputs.

Numerical stability

When this process is implemented on a computer, the vectors u_k are often not quite orthogonal, due to rounding errors. For the Gram–Schmidt process as described above (sometimes referred to as “classical Gram–Schmidt”) this loss of orthogonality is particularly bad; therefore, it is said that the (classical) Gram–Schmidt process is numerically unstable.

The Gram–Schmidt process can be stabilized by a small modification. Instead of computing the vector u_k as

$mathbf{u}_k = mathbf{v}_k - mathrm{proj}_{mathbf{u}_1},(mathbf{v}_k) - mathrm{proj}_{mathbf{u}_2},(mathbf{v}_k) - cdots - mathrm{proj}_{mathbf{u}_{k-1}},(mathbf{v}_k),$

it is computed as

$begin{align} mathbf{u}_k^{(1)} &= mathbf{v}_k - mathrm{proj}_{mathbf{u}_1},(mathbf{v}_k), \ mathbf{u}_k^{(2)} &= mathbf{u}_k^{(1)} - mathrm{proj}_{mathbf{u}_2} , (mathbf{u}_k^{(1)}), \ & ,,, vdots \ mathbf{u}_k^{(k-2)} &= mathbf{u}_k^{(k-3)} - mathrm{proj}_{mathbf{u}_{k-2}} , (mathbf{u}_k^{(k-3)}), \ mathbf{u}_k^{(k-1)} &= mathbf{u}_k^{(k-2)} - mathrm{proj}_{mathbf{u}_{k-1}} , (mathbf{u}_k^{(k-2)}). end{align}$

Each step finds a vector $mathbf{u}_k^{(i)}$ orthogonal to $mathbf{u}_k^{(i-1)}$ . Thus $mathbf{u}_k^{(i)}$ is also orthogonalized against any errors introduced in computation of $mathbf{u}_k^{(i-1)}$ . This approach (sometimes referred to as “modified Gram–Schmidt”) gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.

Algorithm

The following algorithm implements the stabilized Gram–Schmidt orthonormalization. The vectors v₁, …, v_k are replaced by orthonormal vectors which span the same subspace.

for j from 1 to k do

for i from 1 to j − 1 do

$mathbf{v}_j leftarrow mathbf{v}_j - mathrm{proj}_{mathbf{v}_{i}} , (mathbf{v}_j)$

(remove component in direction v_i)

next i

$mathbf{v}_j leftarrow frac{mathbf{v}_j}{|mathbf{v}_j|}$ (normalize)

next j

The cost of this algorithm is asymptotically 2nk² floating point operations, where n is the dimensionality of the vectors (Golub & Van Loan 1996, §5.2.8)

2009/11/13

Data integration

http://www.talend.com/index.php

http://www.opcdatahub.com/Home.html

2009/10/27

Internet y la ciencia

Con solo una PC y conexión a Internet es posible participar en esfuerzos científicos de alcance global.

Explorar el universo

En el sitio www.galaxyzoo.org puedes ayudar a los astrónomos a explorar el universo. El sitio contiene un cuarto de millón de imágenes obtenidas por un telescopio robótico ( Sloan Digital Sky Survey) y voluntarios pueden ayudar a clasificar las imágenes.

La búsqueda de número primos

GIMPS provee programas que se pueden usar como screen savers y buscan números primos. Inclusive hay recompensa económica para motivar el desarrollo de esta tecnología a través de EFF Cooperative Computing Awards para el que encuentre primero:

$50,000 por el primer número primo con más de 1,000,000 dígitos decimales ( Apr. 6, 2000).
$100,000 por el primer número primo con más de 10,000,000 dígitos decimales. El 23 de agosto del 2008 la Electronic Frontier Foundation le concedió a GIMPS el premio ($100,000 Cooperative Computing Award) por el primo 45th del tipo Mersenne, 2^43,112,609-1, un número de 12,978,189 dígitos.
$150,000 por el primer número primo con más de 100,000,000 dígitos decimales.
$250,000 por el primer número primo con más de 1,000,000,000 dígitos decimales.

2009/10/24

Nueva edición de las cátedras de Feynman

Reedición del clásico de clásicos. Es discutible su uso como libro de texto pero hasta los profesores se sentaban a oirlo.

The Feynman Lectures on Physics including Feynman’s Tips on Physics: The Definitive and Extended Edition

2009/09/04

La escalabilidad del computo

Cuando estaba en la escuela, hace algunos años, había gran efervescencia sobre el tema del computo paralelo, de hecho mi tesis doctoral es sobre este tema. Recuerdo que comentado sobre las posibilidades del paralelismo con mi asesor, me dijo que desde un punto de vista teórico el computo paralelo no era importante porque no cambiaba los limites de escalabilidad impuestos por los problemas NP.

Ahora nos encontramos en un resurgimiento de los enfoques del computo distribuido debido al abaratamiento del hardware y la cada vez mayor disponibilidad de conexiones de banda ancha. Por lo tanto la cuestión de algoritmos eficientes para problemas NP y la corroboración teórica de NP ǂ P se ha convertido en uno de los problemas primordiales de la teoría y practica del computo.

Referencias

2009/08/31

Optimización de sitios de Internet

Para hablar de optimización es necesario primero definir el criterio de optimalidad. En el caso de sitios de Internet el criterio es trafico y el logro de objetivos específicos.

Un aspecto primordial para la generación de trafico es la colocación del sitio es los buscadores; sin embargo, el logro de objetivos depende de la experiencia del usuario una vez que llega a la pagina: que el usuario encuentre fácilmente lo que esta buscando; que los objetivos del usuario se correlacionen con los objetivos del sitio; que la pagina se cargue dentro de los tiempos tolerados por el usuario.

Algunos lineamientos generales en los que coinciden los expertos:

Mantener el diseño de paginas y del sitio en general lo más simple posible.
Evitar el uso de Flash e imágenes para presentar información.
Usar paginas estáticas en la medida de lo posible en vez de contenido dinámico.
Mantener la navegación del sitio lo más plano posible, con no más de tres niveles.
Enfocar el contenido a temas muy concretos y presentar información relevante y única.
Conseguir ligas de sitios importantes y relevantes con respecto a la temática del sitio.

En términos técnicos los recomendaciones implican, por ejemplo, el uso de CSS para lograr efectos, CSS Sprites, datos embebidos.

Referencias

2009/08/20

Nubes

El continuo abaratamiento de la infraestructura computacional y la omnisciencia de conexiones de banda ancha están generando un cambio de paradigmas en el industria de tecnología de información y se ven nubes acumulándose en el cielo informático.

Referencias

2009/08/15

CSS; la ortogonalidad del contenido y el diseño

Uno de los preceptos fundamentales del diseño es la separación de responsabilidades entre módulos o componentes. Idealmente cada modulo debe tener un sola responsabilidad primaria. En particular, la funcionalidad de un componente debe ser independiente de la interfaz de usuario.

CSS es un medio de aislar el diseño grafico del contenido textual de un documento. Un ejemplo espectacular de la ortogonalidad del contenido y el diseño se puede ver en CSS Zen Garden